BUSQUEDA HEURISTICA POR COSTO UNIFORME Y HEURISTICA PURA

TORRES DE HANOI:

En la imagen se muestra el grafo de la solución, se señala la mejor solución con color morado.

 HANOI COSTO UNIFORME

LISTA	NODO	SUCESORES
I	I	II(1), III(2)
II(1), III(2)	II(1)	IV(2+1)
III(2), IV(3)	III(2)	V(1+2)
IV(3), V(3)	IV(3)	VI(1+3), VII(1+3)
V(3), VI(4), VII(4)	V(3)	VIII(3+2), IX(3+1)
VI(4), VII(4), VIII(5), IX(4)	VI(4)	STOP
VII(4), VIII(5), IX(4)	VII(4)	VI(4+2), VIII(4+1)
VIII(5), IX(4), VI(6), VIII(5)	IX(4)	VIII(4+1)
VIII(5), VI(6), VIII(5), VIII(5)	VIII(5)	VII(5+1)
VIII(5), VI(6), VIII(5), VII(6)	VIII(5)	VII(5+1)
VI(6), VIII(5), VII(6), VII(6)	VIII(5)	IX(5+1)
VI(6),VII(6), VII(6), IX(6)	VI(6)	STOP
VII(6), VII(6), IX(6)	IX(6)	- - - - - - - - - - - -
VII(6), VII(6)	VII(6)	VI(6+2)

 TALLER HANOI
 

Algoritmo Torres de Hanói (Complejidad )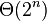

Entrada: Tres pilas de números origen, auxiliar, destino, con la pila origen ordenada Salida: La pila destino si origen  entonces mover el disco 1 de pila origen a la pila destino (insertarlo arriba de la pila destino) terminar si no hanoi(,origen,destino, auxiliar)     //mover todas las fichas menos la más grande (n) a la varilla auxiliar mover disco n a destino                //mover la ficha grande hasta la varilla final hanoi (auxiliar, origen, destino)          //mover todas las fichas restantes, 1...n–1, encima de la ficha grande (n) terminarTORRE 6 DISCOS Se requieren 63 Movimientos 1B-2C-1C-3B-1A-2B-1B-4C-1C-2A-1A-3C-1B-2C-1C- 5B-1A-2B-1B-3A-1C-2A-1A-4B-1B-2C-1C-3B-1A-2B-1B-6C-1C-2A-1A-3C-1B-2C-1C-4A-1A-2B-1B-3A-1C-2A-1A-5C-1B-2C-1C-3B-1A-2B- 1B-4C-1C-2A-1A-3C-1B-2C-1C-

Monótona: No es monótona en todos los nodos porque en el nodo iv es menor el costo estimado que el nodo ancestro.

Admisible: No es admisible en todos los nodos porque  el costo estimado no siempre es menor en el ancestro con respecto a su nodo generado. 

Consistente: Es consistente porque el nodo n no tiene su costo estimado más grande que el costo estimado de su nodo generado.


CÓDIGO EN C

#include <iostream>

using namespace std;

void hanoi(int num,char A,char C,char B)

{

        if(num==1)

        {

                        cout<<"Mueva el bloque "<<num<<" desde "<<A<<" hasta  "<<C<<endl;

                        

        }

        else

        {

                hanoi(num-1,A,B,C);

                cout<<"Mueva el bloque "<<num<<" desde "<<A<<" hasta  "<<C<<endl;

                hanoi(num-1,B,C,A);

        }

}

int main()

{

                int n;

                char A,B,C;

                cout<<"Las torres son A B C\n";

                cout<<"Numero de discos: ";

                cin>>n;

                hanoi(n,'A','C','B');

                

}

REFERENCIAS:

http://www.reglasdel.com/2011/03/torre-de-hanoi.html

http://cremasbasicasytutoriales.blogspot.com.co/